Задачный конкурс журнала Квантик. III тур

Приглашаем всех попробовать свои силы в нашем конкурсе.

Задачи конкурса печатаются в каждом номере и на сайте. Итоги будут подведены в конце года. Участвовать можно, начиная с любого тура. Победителей ждут дипломы журнала «Квантик», научно-популярные книги, диски с увлекательными математическими мультфильмами.

Конкурс ориентирован на школьников 5-8 классов, но и младшеклассники могут присылать решения. Высылайте решения задач III тура, с которыми справитесь, не позднее 5 апреля по электронной почте kvantik@mccme.ru или обычной почтой по адресу: 119002, Москва, Б. Власьевский пер., д. 11, журнал «Квантик». В письме кроме имени и фамилии укажите город, школу и класс, в котором вы учитесь, а также обратный адрес.

Желаем успеха!

11. Профессор написал на доске шесть утверждений: 

Сегодня на моей лекции будет меньше 10 студентов. 
Сегодня на моей лекции будет больше 10 студентов. 
Сегодня на моей лекции будет меньше 20 студентов. 
Сегодня на моей лекции будет больше 20 студентов. 
Сегодня на моей лекции будет меньше 30 студентов. 
Сегодня на моей лекции будет больше 30 студентов. 

На лекцию пришло N студентов, после чего профессор написал для каждого своего утверждения, верное оно или нет. Оказалось, что ровно четыре утверждения оказались неверными. Чему равно N? Укажите все возможные ответы.

12. В классе у Коли столько же детей, сколько в классе у Оли. Коля говорит Оле: «У нас в классе мальчиков вдвое больше, чем у тебя». А Оля отвечает: «Зато у нас девочек втрое больше, чем у тебя». Могло ли такое быть? (Коля и Оля себя тоже посчитали).

13. Перед вами рисунок «капли» – верхняя граница состоит из полуокружности радиуса 2, а нижняя граница – из двух полуокружностей радиуса 1 (одна «смотрит» внутрь капли, а другая – «наружу»).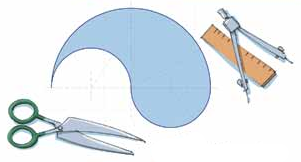 



Разрежьте каплю  а) на две одинаковые части;  б) на три одинаковые части;  в) можно ли разрезать её на 100 равных частей?

14. В таблице 10 x 10 клетки окрашены в 9 цветов. Если в некоторой строке или в некотором столбце находятся две клетки одного цвета, то можно перекрасить этот столбец или эту строку в этот цвет. Из любого ли исходного положения можно всю таблицу перекрасить в один цвет?

15. Бизнесмен заключил с чёртом соглашение: каждый день бизнесмен даёт чёрту одну купюру, а взамен получает любое число купюр, какое захочет, но меньшего достоинства. Другого источника купюр у бизнесмена нет. Докажите, что в какой-то момент бизнесмен разорится (сколько бы купюр ни было у него вначале и как бы он ни менял их у чёрта).