Задачи Сергея Маркелова: увлекательная геометрия и не только

Сергей Маркелов предложил множество интересных задач по математике (только на problems.ru можно найти около 50). Часто парадоксальных — казалось, что добиться требуемого в задаче невозможно… и все-таки в конце концов оказывалось, что решение есть. Не раз приход Сергея практически срывал работу методкомиссии той или иной олимпиады — все бросали остальные дела и начинали решать его новую задачу (а это редко заканчивалось быстро).

Что не менее важно, многие задачи не были изолированными головоломками, они связаны с интересной математикой, часто с нерешенными вопросами. Так что мы приводим не только задачи, но и небольшие комментарии, иногда ссылки на популярные статьи.

Эта задача предлагалась на Математическом празднике 2001 года. Понять, почему это число никак не может быть простым, несложно (попробуйте!). И при этом от нее возникает мостик к разным содержательным (в том числе, нерешенным) вопросам математики — в данном случае, про простые числа Мерсенна (см. статью «Простые числа Мерсенна» в №1 журнала «Квантик» за 2025 год).

Задача предлагалась в 2007 году на олимпиаде по геометрии им. И. Ф. Шарыгина. Конечно, опытные автомобилисты знают, как именно правильно выставлять зеркала. Но такой опыт тут совсем не обязателен — задачу можно решать как задачу по геометрии. Это и предлагается сделать.

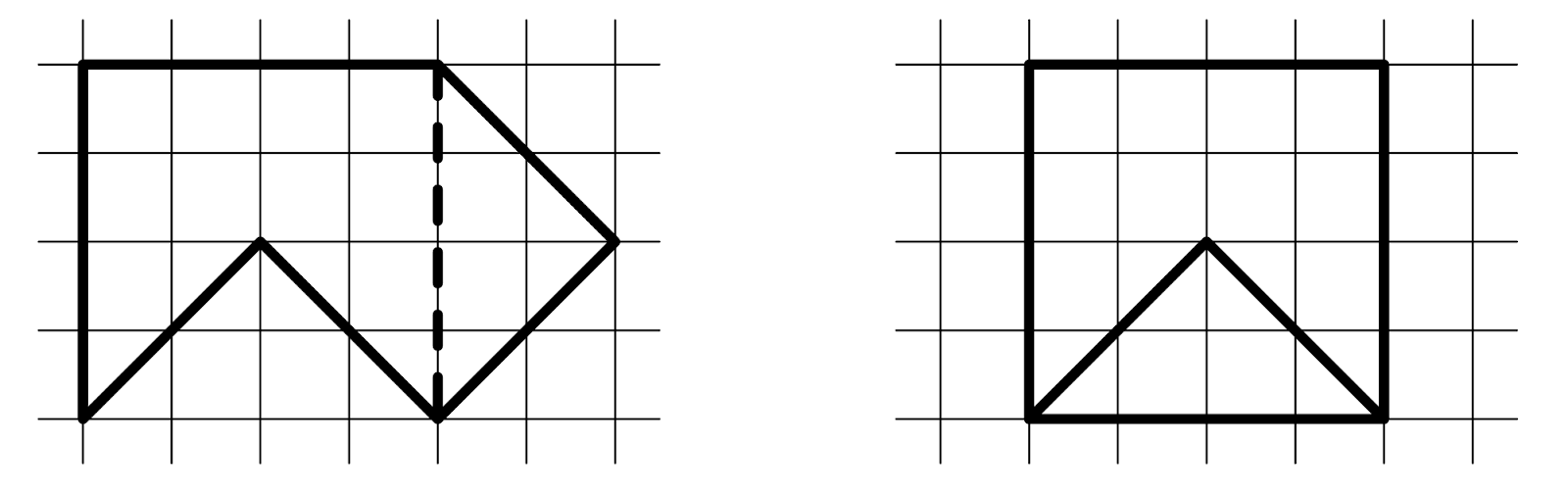
Задача предлагалась на Московской математической олимпиаде 2006 года. Условие понятно любому — но мало кто справился с этой задачей на олимпиаде. Неожиданно, что резать приходится не по клеточкам.

Задача предлагалась на Московской устной олимпиаде по геометрии 2005 года. Полюбуйтесь одним из замощений — и попробуйте придумать другие. Интересно, что такими пятиугольниками можно замостить плоскость непериодически (пример на рисунке: это замощение нельзя сдвинуть так, чтобы оно совпало с собой), но можно и периодически. Многоугольник, которым можно замостить плоскость, но только непериодически, был открыт только в 2024 году (см. по этому поводу статью «Апериодическая плитка» в №11 журнала «Квантик» за 2024 год).

Задача предлагалась на Московской математической олимпиаде 2004 года.

Ответ: да, может! Это выглядит тем более удивительно, что без вложенных радикалов ничего подобного не бывает: например, корень из одного простого числа нельзя представить в виде суммы корней из других простых чисел с рациональными коэффициентами (см., например, статью «Линейная независимость радикалов» в Кванте №3 за 2021 год).

Задача предлагалась на Турнире городов 2003 года. Чтобы понять, как вообще устроены «расстояния с точки зрения муравья», попробуйте для начала разобраться, как устроен кратчайший путь по поверхности куба из вершины в противоположную (по поводу «путей муравья» и связанных вопросов см. также статью «Кратчайшие пути и гипотеза Пуанкаре» в №11-12 за 2020 год и №1 за 2021 год журнала «Квант»).

Задача предлагалась на Московской математической олимпиаде 2005 года. Одно из решений приведено ниже, но сначала — авторский комментарий.

«Данная задача приоткрывает дверь в волшебный мир открытых проблем современной геометрии — ибо если начать смотреть чуть глубже в любом направлении, возникает нерешенная проблема. Укажем некоторые направления возможного исследования:

1) Круг разделен на 12 равных частей так, что центр лежит на границе некоторых, но не всех частей. Верно ли, что части равны частям, получающимся при одном из разрезаний, указанных в решении? Никто не знает!

2) При каких n круг можно разделить на n равных частей так, чтобы центр лежал на границе некоторых, но не всех частей? (Пример известен лишь при n вида 6k, k>2; недавно наш соотечественник А.Я.Канель-Белов доказал, что при n=2 такое деление невозможно, больше ничего не известно).

3) Круг разделен на несколько равных частей. Верно ли, что диаметр каждой из частей не меньше радиуса круга? Никто не знает! (Диаметром фигуры, отличной от круга, называют наибольшее из расстояний между ее точками.)

4) Можно ли разделить круг на несколько равных частей так, чтобы центр круга лежал строго внутри (не на границе) одной из частей? Ответ на этот вопрос не известен не только для круга, но и для правильных n-угольников при n>4.

5) Аналогичные вопросы можно поставить про шар в пространстве. Там не известно ни одного ответа (в том числе и на вопрос, аналогичный поставленному на олимпиаде).»

Кое-что с тех пор стало известно. По поводу вопроса 1 см. заметку «Разрезания круга на равные части» в №3 журнала «Квантик» за 2022 год, по поводу вопроса 4 — заметку «Не разрежь центр» в №1 журнала «Квантик» за 2022 год.