Избранные задачи журнала «Квантик»: для самых любознательных
| Редакция сайта 19 сентября 2025 |
Выпуск № 3 от марта 2026 года
Космонавты и лента
Автор: Александр Бердников. Художник: Алексей Вайнер.
Два космонавта, находящиеся в невесомости за бортом корабля, соединены длинной лентой, концы которой жестко прикреплены к их скафандрам. Лента перекрутилась, что привело к техническим неполадкам, и космонавты потеряли всякую возможность двигаться, неподвижно зависнув друг напротив друга. Отважный Квантик может передвигаться в невесомости и хочет помочь космонавтам по возможности распрямить ленту. Как ему это сделать? (Изменять положение космонавтов он тоже не может)
Узнать, как собрать фонтан, работающий без электричества, прочитать про усвоение лактозы и посмеяться над математическими шутками можно в новом номере журнала «Квантик»!
Ответ на задачу будет опубликован в апреле!
Выпуск № 2 от февраля 2026 года
Смятая бутылка
Художник: Алексей Вайнер.
А узнать, как применить химические знания к сельскому хозяйству, составить из двух узлов один, разгадать анаграммы и склеить ленту Мёбиуса из бумаги можно в новом номере журнала «Квантик»!
Выпуск № 1 от января 2026 года
Декоративная ёлочка
Автор: Михаил Евдокимов. Художник: Татьяна Долгая.
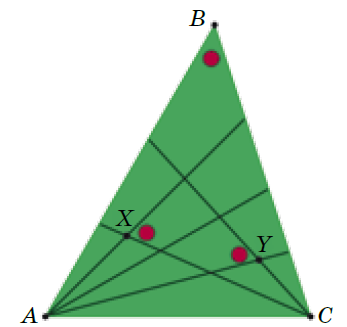
Декоративная новогодняя ёлочка имеет форму треугольника ABC. Из вершин A и C идут гирлянды вдоль лучей, которые делят каждый из углов A и C на равные части. Оказалось, что углы, отмеченные на рисунке красными шарами, равны. Чему равны углы треугольника ABC?
А прочитать про обитателей тундростепи, решить геометрические задачи и разгадать календарь-головоломку можно в новом номере журнала «Квантик»!
Выпуск № 12 от декабря 2025 года
Лыжные палки
Художник: Алексей Вайнер.
По картинке определите, соприкасаются ли эти лыжные палки.
По мотивам журнала «Квант»
А узнать про нового родственника жирафа, распутать головоломку «меледа́» и провести эксперимент с обычным полиэтиленовым пакетом можно с помощью декабрьского номера журнала «Квантик»!
Выпуск № 11 от ноября 2025 года
Чуть не проворонил
В Муромском лесу на каждом дереве сидело, по крайней мере, по одной вороне. Когда Соловей-разбойник засвистел, вороны, испугавшись, взлетели, а когда свист прекратился, они, полетав по лесу, вновь расселись по деревьям. При этом оказалось, что после свиста расстояние между каждыми двумя воронами уменьшилось. (Под расстоянием между воронами мы понимаем расстояние между деревьями, на которых они сидят.) Докажите, что хотя бы одна ворона вернулась на то же дерево, на котором она находилась до свиста Соловья-разбойника.
Прочитать о загадочных облаках, узнать про суперсилу шахматной ладьи и самостоятельно собрать модель ромбокубооктаэдра можно с помощью журнала «Квантик»!
Выпуск № 10 от октября 2025 года
Узнать, как разделить прямоугольный лист бумаги на три части, построить жесткие многоугольники из конструктора и прочитать о том, как в Европу привозили носорогов, можно в октябрьском номере журнала «Квантик»!
Выпуск № 9 от сентября 2025 года
Велосипедисты и муха
Узнать, как искать пифагоровы тройки, рисовать додекаэдр и почему светятся лампочки, можно в сентябрьском номере журнала «Квантик»!
Ответы
Ответ на сентябрьскую задачу «Велосипедисты и муха»:
1. Велосипедисты встретятся в середине отрезка АБ, то есть каждый проедет по 5 км и потратит на это 0,5 ч. Муха летает со скоростью 20 км/ч, следовательно, пролетит 10 км.
2. Рассмотрим движение мухи после того, как она пролетит 5 км до середины АБ. Закончит свое движение муха в этой же точке, следовательно, в направлении от А к Б пролетит столько же, сколько и от Б к А. То есть в направлении от А к Б муха пролетит 5+5/2 = 7,5 км, а в направлении от Б к А пролетит 5/2=2,5 км.
3. В направлении от А к Б муха пролетит (5 + х) км и потратит на это (5 + х)/22 часов, а в направлении от Б к А – х км и потратит х/18 часов. Велосипедисты до встречи в центре АБ ехали 0,5 ч, следовательно (5+х)/22+х/18=0,5. Умножим на 2•11•9 обе части равенства: 45 + 9х + 11х = 99, значит, 20х = 54 или х = 2,7. Муха пролетит 5+2х=10,4 км.
Ответ на октябрьскую задачу «Космический молоток»:
Боёк обычного молотка (та часть, которой ударяют по чему-либо) делается из цельного куска металла. Он жёсткий и поэтому хорошо отскакивает. Зато совсем не отскакивают при ударе мягкие предметы: пластилин или, скажем, мешок с песком. Из пластилина, конечно, молоток не сделаешь, а вот вторую идею использовать можно: надо сделать боёк молотка полым и насыпать в него песок. В реальности вместо песка обычно используют маленькие металлические шарики, чтобы повысить массу молотка и силу удара. Такие молотки (их называют безынерционными) используются не только в космосе, но и на Земле – тогда, когда требуется точно контролировать силу удара, например при выравнивании вмятин на кузове автомобиля.
Ответ на ноябрьскую задачу «Чуть не проворонил»:
Тому, кто считает, что два дерева для Муромского леса – как-то маловато (больше похоже не
на дремучий лес, а на Лысую гору), можно предложить другую схему. Пусть через лес проведена
(мысленно!) прямая линия, и каждому дереву по одну сторону от неё соответствует симметрично
расположенное дерево по другую сторону (а на самой прямой деревьев нет). Если после свиста
каждая ворона перелетела на симметричное дерево, то итоговое расположение ворон окажется зеркальным по отношению к исходному, и расстояние между каждой парой ворон не изменится.
Ответ на декабрьскую задачу «Лыжные палки»:
Верхний конец палки, его тень и солнце лежат на одной прямой. Палок две, получаем две прямые. Пусть палки соприкасаются. Тогда есть третья прямая, на которой лежат точка соприкосновения палок, солнце и точка пересечения теней. Эти три прямые должны пересекаться в одной точке – там, где находится солнце. Но видно, что третья прямая (точнее, ее продолжение) пересекает на картинке первые две прямые в двух разных точках, противоречие! Значит, палки не соприкасаются.
Ответ на январскую задачу «Декоративная ёлочка»:
Пусть ∠A = 4a, ∠C = 3с. Один красный шар расположен в вершине B. Обозначим вершины углов,
которые отмечены двумя другими шарами, как X и Y (см. рисунок). Тогда шары расположены
во внешних углах треугольников ACX и ACY.
Внешний угол в треугольнике равен сумме двух углов, не смежных с ним. Поэтому можно записать равенство 3a + c = a + 2c. Отсюда, c = 2a и каждый из углов X, Y равен 5a.
Угол B по условию тоже равен 5a, а также он равен 180° – ∠A – ∠C = 180° – 4a – 3c = 180° – 10a.
Значит, 5a = 180° – 10a и a = 12°. Тогда c = 24°, откуда получаем ответ: ∠A = 48°, ∠С = 72°, ∠B = 60°.
Ответ на февральскую задачу «Смятая бутылка»:
На вершине горы давление воздуха меньше, чем у подножия. Находясь наверху, Саша отпил часть воды из бутылки и запустил внутрь нее воздух под небольшим давлением. А когда Саша спустился, воздух снаружи сдавил более разреженный воздух внутри бутылки, и она оказалась помятой.