«Сорок детей водили хоровод»: любимые задачи организаторов Матпраздника

6 класс, 2002 год, автор И. Ф. Акулич
Художник-авангардист Змий Клеточкин покрасил несколько клеток доски размером 7×7, соблюдая правило: каждая следующая закрашиваемая клетка должна соседствовать по стороне с предыдущей закрашенной клеткой, но не должна соседствовать ни с одной другой ранее закрашенной клеткой. Ему удалось покрасить 31 клетку.

Побейте его рекорд – закрасьте а) 32 клетки; б) 33 клетки.

7 класс, 2002 год, автор А. С. Чеботарев
Художник-авангардист Змий Клеточкин покрасил несколько клеток доски размером 8×8, соблюдая правило: каждая следующая закрашиваемая клетка должна соседствовать по стороне с предыдущей закрашенной клеткой, но не должна – ни с одной другой ранее закрашенной клеткой. Ему удалось покрасить 36 клеток. Побейте его рекорд! (Жюри умеет закрашивать 42 клетки!)

6 класс, 2007, автор И. В. Раскина
Кощей Бессмертный похитил у царя трех дочерей. Отправился Иван-царевич их выручать. Приходит он к Кощею, а тот ему и говорит: «Завтра поутру увидишь пять заколдованных девушек. Три из них – царевы дочери, а еще две – мои. Для тебя они будут неотличимы, а сами друг дружку различать смогут. Я подойду к одной из них и стану у нее спрашивать про каждую из пятерых: "Это царевна?". Она может отвечать и правду, и неправду, но ей дозволено назвать царевнами ровно двоих (себя тоже можно называть). Потом я так же опрошу каждую из остальных девушек, и они тоже должны будут назвать царевнами ровно двоих. Если после этого угадаешь, кто из них и вправду царевны, отпущу тебя восвояси невредимым. А если еще и догадаешься, которая царевна старшая, которая средняя, а которая младшая, то и их забирай с собой». Иван может передать царевнам записку, чтобы научить их, кого назвать царевнами. Может ли он независимо от ответов Кощеевых дочерей:

а) вернуться живым? 
б) увезти царевен с собой?

6 класс, 2012 год, автор А. В. Хачатурян
Известно, что Шакал всегда лжет, Лев говорит правду, Попугай просто повторяет последний услышанный ответ (а если его спросить первым, ответит как попало), а Жираф дает честный ответ, но на предыдущий заданный ему вопрос (а на первый вопрос отвечает как попало). Мудрый Ежик в тумане наткнулся на Шакала, Льва, Попугая и Жирафа и решил выяснить, в каком порядке они стоят. Спросив всех по очереди «Ты Шакал?», он понял только лишь, где Жираф. Спросив всех в том же порядке: «Ты Жираф?», он смог еще понять, где Шакал, но полной ясности так и не наступило. И лишь после того как на вопрос «Ты Попугай?» первый ответил «Да», Ежу, наконец, стало ясно, в каком порядке стояли животные. Так в каком же?

(«Как попало» означает, что один из ответов «Да» или «Нет» выбирается произвольно.)

7 класс, 2001 год, автор А. Шень
В стене имеется маленькая дырка (точка). У хозяина есть флажок следующей формы (см. рисунок).

Покажите на рисунке все точки, в которые можно вбить гвоздь, так чтобы флажок закрывал дырку.

7 класс, 2003 год, автор А. С. Чеботарев
Квадратную салфетку сложили пополам, полученный прямоугольник сложили пополам еще раз (см. рисунок). Получившийся квадратик разрезали ножницами (по прямой). Могла ли салфетка распасться а) на 2 части? б) на 3 части? в) на 4 части? г) на 5 частей? Если да – нарисуйте такой разрез, если нет – напишите слово «нельзя».

7 класс, 2012 год, автор И. В. Ященко
Квадрат 3×3 заполнен цифрами так, как показано на рисунке слева. Разрешается ходить по клеткам этого квадрата, переходя из клетки в соседнюю (по стороне), но ни в какую клетку не разрешается попадать дважды.

Петя прошел, как показано на рисунке справа, и выписал по порядку все цифры, встретившиеся по пути, – получилось число 84937561. Нарисуйте другой путь так, чтобы получилось число побольше (чем больше, тем лучше).

7 класс, 2006 год, автор Н. Нетрусова

Наташа сделала из листа клетчатой бумаги календарь на январь 2006 года (см. рисунок) и заметила, что центры клеток 10, 20 и 30 января образуют равнобедренный прямоугольный треугольник. Наташа предположила, что это будет верно и в любом другом году, за исключением тех лет, когда центры клеток 10, 20 и 30 лежат на одной прямой. Права ли Наташа?

7 класс, 2013 год, автор А. В. Шаповалов

Три квадратные дорожки с общим центром отстоят друг от друга на 1 м (см. рис.). Три муравья стартуют одновременно из левых нижних углов дорожек и бегут с одинаковой скоростью: Му и Ра против часовой стрелки, а Вей по часовой. Когда Му добежал до правого нижнего угла большой дорожки, двое других, не успев ещё сделать полного круга, находились на правых сторонах своих дорожек, и все трое оказались на одной прямой. Найдите стороны квадратов.

Вифсла, Тофсла и Хемуль играли в снежки. Первый снежок бросил Тофсла. Затем в ответ на каждый попавший в него снежок Вифсла бросал 6 снежков, Хемуль – 5, а Тофсла – 4. Через некоторое время игра закончилась. Найдите, в кого сколько снежков попало, если мимо цели пролетели 13 снежков. (В себя самого снежками не кидаются и один снежок не может попасть в двоих).

6 класс, 2012 год, автор И. В. Раскина

Торт упакован в коробку с квадратным основанием. Высота коробки вдвое меньше стороны этого квадрата. Ленточкой длины 156 см можно перевязать коробку и сделать бантик сверху (как на рисунке слева). А чтобы перевязать ее с точно таким же бантиком сбоку (как на рисунке справа), нужна ленточка длины 178 см. Найдите размеры коробки.

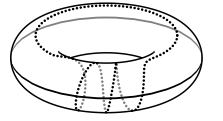
7 класс, 2016 год, авторы С. К. Смирнов, И. В. Ященко

По поверхности планеты, имеющей форму бублика, проползли, оставляя за собой следы, две улитки: одна по внешнему экватору, а другая по винтовой линии (см. рис.). На сколько частей разделили поверхность планеты следы улиток? (Достаточно написать ответ.)

7 класс, 1999 год

Два пешехода вышли на рассвете. Каждый шел с постоянной скоростью. Один шел из A в B, другой – из B в A. Они встретились в полдень и, не прекращая движения, пришли: один – в B в 4 часа вечера, а другой – в A в 9 часов вечера. В котором часу в тот день был рассвет?

Эта задача была отобрана В. И. Арнольдом в его замечательный сборник «Задачи от 5 до 15 лет».

6 класс, 1997 год

Семья ночью подошла к мосту. Папа может перейти его за 1 минуту, мама – за 2, малыш – за 5, а бабушка – за 10 минут. У них есть один фонарик. Мост выдерживает только двоих. Как им перейти мост за 17 минут? (Если переходят двое, то они идут с меньшей из их скоростей. Двигаться по мосту без фонарика нельзя. Светить издали нельзя. Носить друг друга на руках нельзя.)